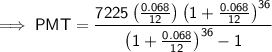Answer:
Option 1: $261.68 per month
Option 2: $222.43 per month
Explanation:
APR = Annual Percentage Rate and is the stated interest rate of the loan averaged over 12 months. APR is typically applied to money that is borrowed, e.g. credit card, car loan, personal loan, home loan or student loan.
When paying off a loan with equal monthly payments, with each payment the principal owed is reduced which results in a decreasing interest due.
Monthly Payment Formula
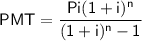
where:
- PMT = monthly payment
- P = loan amount
- i = interest rate per month (in decimal form)
- n = term of the loan (in months)
Option 1
Given:
- P = $8500
- i = 0.068 ÷ 12
- n = 36
Substitute the given values into the formula and solve for PMT:
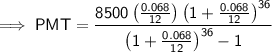

Option 2
Given:
- P = $8500 - 15% = $7225
- i = 0.068 ÷ 12
- n = 36
Substitute the given values into the formula and solve for PMT: