Question 1
If we let
 , then
, then
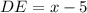 .
.
Also, as
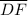 bisects
bisects
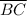 , this means
, this means
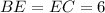 .
.
Thus, by the intersecting chords theorem,

However, as distance must be positive, we only consider the positive case, meaning FE=9
Question 2
If we let CE=x, then because AB bisects CD, CE=ED=x.
We also know that since FB=17, the radius of the circle is 17. So, this means that the diameter is 34, and as AE=2, thus means EB=32.
By the intersecting chords theorem,
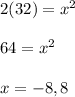
However, as distance must be positive, we only consider the positive case, meaning CE=8