Question

Item 4 Question 1 Determine of which lines, if any, are parallel or perpendicular. Explain. Line a passes through (−2, 1) and (0, 3) . Line b passes through (4, 1) and (6, 4) . Line c passes through (1, 3) and (4, 1) .

Answer 1

Line b and line c are perpendicular.

Explanation:

In order to find if the lines are parallel, perpendicular or neither, their slopes have to be found.

Slope is denoted by m and is calculated as:

`m = (y_2-y_1)/(x_2-x_1)`

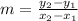
Here (x1,y1) and (x2,y2) are the coordinates of the point through which the line passes.

Let m1 be the slope of line a

and line a passes through (−2, 1) and (0, 3)

`m_1 = (3-1)/(0+2) = (2)/(2) = 1`

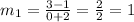
Let m2 be the slope of line b which passes through (4, 1) and (6, 4)

`m_2 = (4-1)/(6-4) = (3)/(2)`

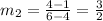
Let m3 be the slope of line c which passes through (1, 3) and (4, 1)

`m_3 = (1-3)/(4-1) = (-2)/(3)`

When two lines are parallel, their slopes are equal.

When two lines are parallel, the product of their slope is -1

None of the slopes are equal to each other so none of the lines are parallel

And

`m2.m3\\= (3)/(2) * -(2)/(3)\\= -1`

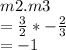
Hence,

Line b and line c are perpendicular.