Question

Answer the following:

21. Are the following equations parallel, perpendicular or neither?
-3x + y = -4
x + 3y = 6

Answer 1

As the product of the slop of both lines is -1.

• 
  `m_1* m_2=-1`

• 
  `3* (-1)/(3)=-1`

Therefore, the given equations are perpendicular.

Explanation:

Given the equations

`-3x+y=-4`

`x+3y=6`

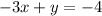
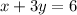
The slope-intercept form of the equation is

`y=mx+b`

where m is the slope and b is the y-intercept.

Writing both equations in the slope-intercept form

`-3x+y=-4`

`y=3x-4`

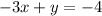
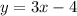
So by comparing with the slope-intercept form we can observe that

slope of equation = 3

i.e.

`m_1=3`

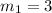
also

`x + 3y = 6`

`3y\:=\:6-x`

`y=-(1)/(3)x+2`

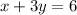
So by comparing with the slope-intercept form we can observe that

the slope of equation = -1/3

i.e.

`m_2=-(1)/(3)`

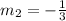
as

The slope of the perpendicular line is basically the negative reciprocal of the slope of the line.

so

The slope
`m_2` is the negative reciprocal of the slope
`\:m_1`

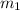
Also, the product of two perpendicular lines is -1.

i.e.

`m_1* m_2=-1`

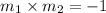
VERIFICATION:

It is clear that the product of the slop of both lines is -1.

`m_1* m_2=-1`

`3* (-1)/(3)=-1`

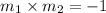
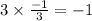
Therefore, the given equations are perpendicular.