Question

Lily is building a triangular garden in her backyard. She is going to use 2x yards of fencing for the width and 50x yards of fencing for the height of the triangular garden. She thinks the maximum area of the garden is 625 yards. Do you agree or disagree with Lily? ​

Answer 1

There is no critical point associated with a maximum area of the triangle.

Explanation:

From Geometry we understand that the area of the triangle is defined by the following formula:

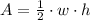`A = (1)/(2)\cdot w\cdot h` (1)

Where:

`A` - Area, measured in square yards.

`w` - Width, measured in yards.

`h` - Height, measured in yards.

From statement the following relationships are known:

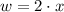`w = 2\cdot x` (2)

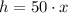`h = 50\cdot x` (3)

By applying (2) and (3) in (1) we obtain this expression:

`A = (1)/(2)\cdot (2\cdot x)\cdot (50\cdot x)`

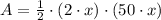
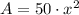`A = 50\cdot x^(2)` (4)

Now we perform First and Second Derivative Test on the resulting expression:

First Derivative Test

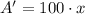`A' = 100\cdot x` (5)

`100\cdot x = 0`

`x = 0\,yd`

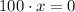
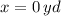
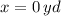`x = 0\,yd` is a critical point of (4).

Second Derivative Test

`A'' = 100` (6)

The critical point leads to an absolute minimum. According to this analysis, there is no critical values associated to maximum area.