Question

If 1.0 mol of N2 and 3.0 mol of H2 in a closed container initially at STP react completely in the reaction shown below, then the final pressure in the flask will be ________ atm at 273 K.

Answer 1

`p_f=0.5atm`

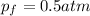
Step-by-step explanation:

Hello!

In this case, since the reaction between nitrogen and hydrogen produces ammonia:

`N_2+3H_2\rightarrow 2NH_3`

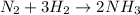
We can compute the volume of the container by using the ideal gas law at STP (1 atm and 273.15 K):

`V=(4.0mol*0.08206(atm*L)/(mol*K)*273.15K)/(1atm)=89.7L`

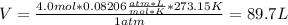
Next, since nitrogen and hydrogen are in a 1:3 mole ratio, we understand all the nitrogen and hydrogen are consumed and only ammonia remains at the end of the reaction in the following amount:

`n_(NH_3)=1.0molN_2*(2molNH_3)/(1molN_2) =2.0molNH_3`

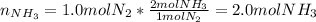
Thus, the final pressure turns out:

`p_f=(2.0mol*0.08206(atm*L)/(mol*K)*273.15K)/(89.7L)\\\\p_f=0.5atm`

Best regards!