Question

water flows into a reservoir at a rate of 1500+7t^2 gallons/hour. Since there is a tiny hole in the reservoir, the water leaks out at a rate of 4t+t^2 gallons/hour. What is the net change in the amount of water in the reservoir over the time interval of [1,5]

Answer 1

9514 1404 393

Answer:

6200 gallons

Explanation:

The rate of change of volume is the difference between the inflow rate and the outflow rate.

v'(t) = (1500 +7t^2) -(4t +t^2) = 6t^2 -4t +1500

The change in volume over the time interval of interest is the integral of this expression over that interval:

`\displaystyle\Delta V=\int_1^5{(6t^2-4t+1500)}\,dt=\left.(2t^3-2t^2+1500t)\right|^5_1\\\\=2(5^3-1^3)-2(5^2-1^2)+1500(5-1) = 2\cdot124-2\cdot24+1500\cdot4\\\\\boxed{\Delta V=6200\qquad\text{gallons}}`

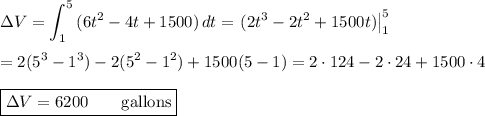
The amount of water in the reservoir increases by 6200 gallons over the time interval.