Question

\sqrt{53+20\sqrt{7}} can be written in the form a+b\sqrt{c}, where a, b, and c are integers and c has no factors which is a perfect square of any positive integer other than 1. Find a+b+c.

Answer 1

Answer: 14

=====================================================

Step-by-step explanation:

Since the range of
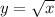`y = √(x)` is
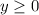`y \ge 0`, this means that
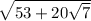`\sqrt{53+20√(7)}` cannot be negative.

-----------------------------------

Let's set the given nested radical expression equal to the form a+b*sqrt(c), and then square both sides to see what happens

`\sqrt{53+20√(7)} = a+b√(c)\\\\\left(\sqrt{53+20√(7)}\right)^2 = \left(a+b√(c)\right)^2\\\\53+20√(7) = a^2+2ab√(c)+b^2c\\\\53+20√(7) = (a^2+b^2c)+2ab√(c)\\\\`

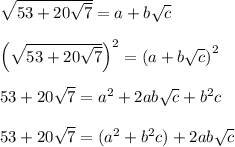
Equating the corresponding parts shows that

`53=a^2+b^2c \text{ and } 20√(7) = 2ab√(c)\\\\`

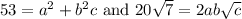
Therefore c = 7 must be the case to allow the radicands to match up.

-----------------------------------

Since c = 7, we can update the first equation like so

`53=a^2+b^2c\\\\53=a^2+b^2*7\\\\53=a^2+7b^2\\\\`

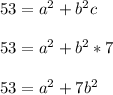
We'll come back to this later.

-----------------------------------

Focus on
`20 = 2ab√(7)`

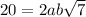
Note how 20 and 2ab are coefficients outside the root. So 20 = 2ab leads to ab = 10.

Here are all the ways to multiply to 10 where a,b are integers

• 1*10 = 10
• -1*(-10) = 10
• 2*5 = 10
• -2*(-5) = 10

So we could have these possibilities.

• a = 1, b = 10
• a = 10, b = 1
• a = -10, b = -1
• a = -1, b = -10
• a = 2, b = 5
• a = 5, b = 2
• a = -5, b = -2
• a = -2, b = -5

If you try all of those a,b combinations with
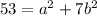`53 = a^2 + 7b^2`, then you should find that a = 5 and b = 2 works. I'm skipping a bunch of steps here. All you basically do is plug and chug.

Due to symmetry, we could have a = -5 and b = -2 as another solution to
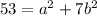`53 = a^2 + 7b^2`. However, if a < 0 and b < 0, then
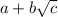`a+b√(c)` would be negative which contradicts the fact that
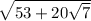`\sqrt{53+20√(7)}` is positive. So we'll ignore any case where a,b are negative.

Therefore, the only combination that works is a = 5 and b = 2

-----------------------------------

Overall, we found that

• a = 5
• b = 2
• c = 7

And therefore,

`\sqrt{53+20√(7)} = a+b√(c)\\\\\sqrt{53+20√(7)} = 5+2√(7)\\\\`

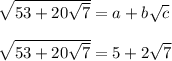
You can confirm this with your calculator by taking advantage of the idea "If x = y, then x-y = 0". In other words, if you subtract the left and right sides, you should get 0 as a result (the order of subtraction doesn't matter in this case). Don't forget to use parenthesis correctly, or you may not get 0. It might help to think of it as the form (x) - (y) = 0.

After we confirmed we have the correct a,b,c values, we simply add them up to get a+b+c = 5+2+7 = 14.