Hi student, let me help you out!
..................................................................................................................
----------------------------------------------
Part 1.
What is the slope of the line
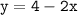 ?
?
---------------------------------------------
Part 2.
What is the slope of the line that is parallel to the line
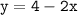 ?
?
- slope =
The slopes of parallel lines are identical.
----------------------------------------------------
Part 3. Equation
Now that we've found the slope, we can easily find the equation.
Recall the point that the line contains: (2, -1).
Let's stick in its y-coordinate, -1, instead of y:
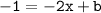
Do the exact same thing with x:
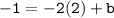 .
.
Upon simplifying, we obtain
 .
.
Now we should add 4 to both sides:
 .
.
Upon simplifying, we obtain
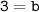
- Incase you're wondering, "b" is the y-intercept.
∴, the equation of the line is
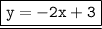 .
.
Hope this helped you out, ask in comments if any queries arise.
Best Regards!

