Question

Test the hypothesis using the​ P-value approach. Be sure to verify the requirements of the test. Upper H 0​: pequals0.6 versus Upper H 1​: pgreater than0.6 nequals200​; xequals135​, alphaequals0.05 Is np 0 (1 minus p 0 )greater than or equals​10.

Use technology to find the P-Value.

Answer 1

Explanation:

From the given information:

The null and the alternative hypothesis can be well written as:

`H_o:P=0.6`

`H_1:P>0.6`

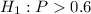
Given that:

n = 200

x = 135

Alpha ∝ = 0.05 level of significance

Then;

⇒
`n * p* (1-P)`

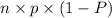
= 200 × 0.6 × (1 -0.6)

= 200 × 0.6 × 0.4

= 48 ≥ 10

The sample proportion
`\hat P = (x)/(n)`

`= (135)/(200)`

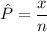
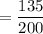
= 0.675

The test statistics
`Z = \frac{\hat P - P}{\sqrt{ (P(1-P))/(n) }}`

`Z = \frac{0.675 - 0.6}{\sqrt{ (0.6 * 0.4)/(200) }}`

`Z = \frac{0.075}{\sqrt{ (0.24)/(200) }}`

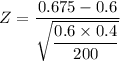
Z = 2.165

The P-value = P(Z > 2.165)

= 1 - P(Z < 2.165)

From the z tables

= 1 - 0.9848

= 0.0152

Reject the null hypothesis since P-Value is lesser than alpha. ( i.e. 0.0152 < 0.05).

Thus, there is enough evidence to conclude that the value of the population proportion is greater than 0.6