Answer:
1. The value of the variable, y is 11
2. (B) QRS is congruent to segment (E) ΔWXY by the hypotenuse leg congruency criteria
Explanation:
1. The lengths of the sides of the given triangles ABC are AB = 14, BC = 27, AC = 19, and ∡A = 32°
The lengths of the sides of the given triangle FGH, FG = 14, GH = 19, FH = 2y + 5, ∡G = 32°
From the given parameters, we have;
Segment AB (AB = 14) is congruent to segment FG (FG = 14)
Segment AC (AC = 19) is congruent to segment GH (GH = 19)
Angle ∡A (∡A = 32°) is congruent to angle ∡G (∡G = 32°)
∴ ΔBAC is congruent to ΔFGH by the Side-Angle-Side rule of congruency
Therefore, segment BC is congruent to segment FH by Congruent Parts of Congruent Triangle are Congruent, CPCTC
Segment BC = Segment FH by definition of congruency
∴ 27 = 2·y + 5
2·y + 5 = 27
2·y = 27 - 5 = 22
y = 22/2 = 11
y = 11
The value of the variable, y = 11
2. For option A. the vertices of triangle ABC are A(-7, 4), B(-4, 1), C(-2, 5)
The length of the sides are;
The length of side AB = √((-4 - (-7))² + (1 - 4)²) = 3·√2
The length of side BC = √((-4 - (-2))² + (1 - 5)²) = √20
The length of side AC = √((-2 - (-7))² + (5 - 4)²) = √26
For option B. the vertices of triangle QRS are Q(3, -4), R(3, -1), S(7, -1)
The length of the sides are;
The length of side QR = √((3 - 3)² + ((-4) - (-1))²) = 3
The length of side RS = √((7 - 3)² + (-1 - (-1))²) = 4
The length of side QS = √((3 - 7)² + ((-4) - (-1))²) = 5
For option C. the vertices of triangle DEF are D(-2, 6), E(1, 3), F(3, 7)
The length of the sides are;
The length of side DE = √(((-2) - 1)² + (6 - 3)²) = 3·√2
The length of side EF = √((3 - 1)² + (7 - 3)²) = √20
The length of side DF = √((3 - (-2))² + (7 - 6)²) = √26
For option D. the vertices of triangle TUV are T(-6, -5), U(-6, 1), V(4, 1)
The length of the sides are;
The length of side TU = √(((-6) - (-6))² + ((-5) - 1)²) = 6
The length of side UV = √(((-6) - 4)² + (1 - 1)²) = 10
The length of side TV = √(((-6) - 4)² + ((-5) - 1)²) = 2·√34
For option E. the vertices of triangle WXY are W(-6, 4), X(-6, 1), Y(-2, 1)
The length of the sides are;
The length of side WX = √(((-6) - (-6))² + (4 - 1)²) = 3
The length of side XY = √(((-6) - (-2))² + (1 - 1)²) = 4
The length of side WY = √(((-6) - (-2))² + (4 - 1)²) = 5
Therefore;
Segment QR of ΔQRS is congruent to segment WX of ΔWXY
Segment RS of ΔQRS is congruent to segment XY of ΔWXY
Segment QS of ΔQRS is congruent to segment WY of ΔWXY
Whereby QS and WY are the hypotenuse side of ΔQRS and ΔWXY respectively, because QS = WY = 5 = √(
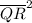 +
+
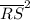 ) = (√(3² + 4²)
) = (√(3² + 4²)
and also RS = XY, by the definition of congruency, we have;
QRS is congruent to segment ΔWXY by the hypotenuse leg congruency criteria