Question

The number of research articles in a prominent journal written by researchers during 1983–2003 can be approximated by U(t) = 4.1e0.6t 0.2 + e0.6t thousand articles per year (0 ≤ t ≤ 20) where t is time in years (t = 0 represents 1983). (a) Find an (approximate) expression for the total number of articles (in thousands) written since 1983 (t = 0). HINT [See Example 5.] (Round your coefficients to two decimal places.) N(t) = (b) Roughly how many articles were written from 1983 to 2003? (Round your answer to the nearest whole number.) thousand articles

Answer 1

Explanation:

From the information given:

We are to find; an expression for the total no. of articles written since 1983

∴

The total no. of articles written since 1983
`=\int \limts ^t_0 U(t) dt`

`= \int ^t_0 \limits (4.1 e^(0.6\ t))/(0.2+e^(0.6t)) \ dt`

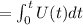
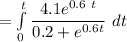
`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(0.6 x) \bigg| \bigg]^t_0`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(0.6 x) \bigg| - \mathtt{In} \bigg|0.2+1\bigg|\bigg]`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | (0.2 + e^(0.6 x))/(1.2) \bigg|\bigg]`

`=(41)/(6) \mathtt{In} \bigg | {0.2 + e^(0.6 x) \bigg|-(41)/(6) \mathtt{ In} \bigg | 1.2\bigg |`

`=6.833* \mathtt{In} \bigg | {0.2 + e^(0.6 x) \bigg|-1.2458`

`=6.833* \mathtt{In} \bigg | {0.2 + e^(0.6 x) \bigg|-1.25 \ \mathbf{thousand \ articles}`

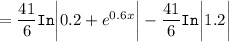
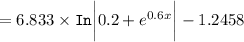
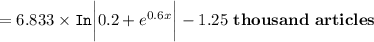
Therefore, the total number of articles written since 1983 is
`=6.833* \mathtt{In} \bigg | {0.2 + e^(0.6 x) \bigg|-1.25 \ \mathbf{thousand \ articles}`

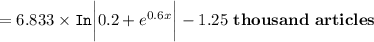
b. To find how many articles were being written from 1983 to 2003

i.e. t = 2003 - 1983 = 20

∴

Total articles written from 1983 to 2003 is
`=\int \limts ^(20)_0 U(t) dt`

`= \int ^(20)_0 \limits (4.1 e^(0.6\ t))/(0.2+e^(0.6t)) \ dt`

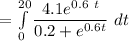
`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(0.6 x) \bigg| \bigg]^(20)_0`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(0.6 *20) \bigg| - \mathtt{In} \bigg|0.2+e^(0.6*0)\bigg|\bigg]`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(12) \bigg| - \mathtt{In} \bigg|0.2+e^0\bigg|\bigg]`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(12) \bigg| - \mathtt{In} \bigg|0.2+1\bigg|\bigg]`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | 0.2 + e^(12) \bigg| - \mathtt{In} \bigg|1.2\bigg|\bigg]`

`=(4.1)/(0.6)\bigg [ \mathtt{In} \bigg | (0.2 + e^(12))/(1.2) \bigg|\bigg]`

= 80.75 thousand articles