Question

What is the midpoint of the line segment with endpoints (-2,-2) and (4, 6)?

Answer 1

(1,2)

Explanation:

(x,y) = ((x1+x2)/2 , (y1+y2)/2)

[substitute values given]

(x,y) = ((-2+4)/2 , (-2+6)/2)

[solve the equation]

(x,y) = (2/2 , 4/2)

[simplify the values]

(x,y) = (1 , 2)

Answer 2

Let's solve ~

We can use section formula to find the mid - point of the given line segment as it divied the line segment into ratio of 1 : 1

Let the coordinates of mid - point be (x , y)

`\qquad \sf  \dashrightarrow \: x = (mx_2 - nx_1)/(m + n)`

`\qquad \sf  \dashrightarrow \: y= (my_2 - ny_1)/(m + n)`

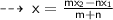
here,

• 
  `\sf{x_1 = -2 }`

• 
  `\sf{y_1 = -2 }`

• 
  `\sf{x_2 = 4 }`

• 
  `\sf{y_2 = 6}`

The ratio is m : n ~ i.e equivalent to 1 : 1, meaning m = n = 1.

`\qquad \sf  \dashrightarrow \: x = (4 - ( - 2))/(1 + 1)`

`\qquad \sf  \dashrightarrow \: x = (4 + 2)/(2)`

`\qquad \sf  \dashrightarrow \: x = (6)/(2)`

`\qquad \sf  \dashrightarrow \: x = 3`

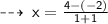
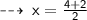
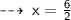
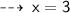
similarly ~

`\qquad \sf  \dashrightarrow \: y= (6 - ( - 2))/(1 + 1)`

`\qquad \sf  \dashrightarrow \: y= (6 + 2)/(2)`

`\qquad \sf  \dashrightarrow \: y= (8)/(2)`

`\qquad \sf  \dashrightarrow \: y = 4`

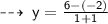
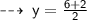
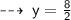
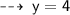
So, the midpoint of the line segment has coordinates:

• (3 , 4)