Answer:
The average rate of change is -18.
Explanation:
We are given the function:
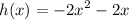
And we want to find its average rate of change from x = 2 to x = 6.
Recall that to find the average rate of change between two points of any functions, we find the slope between the two endpoints. Hence, evaluate the endpoints:
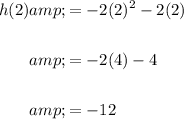
Likewise:
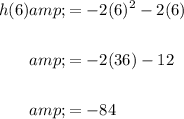
The slope between the two endpoints is therefore:

In conclusion, the average rate of change of h from x = 2 to x = 6 is -18.