Question

There is a spot of paint on the front wheel of the bicycle. Take the position of the spot at time t=0 to be at angle θ=0 radians with respect to an axis parallel to the ground (and perpendicular to the axis of rotation of the tire) and measure positive angles in the direction of the wheel's rotation. What angular displacement θ has the spot of paint undergone between time 0 and 2 seconds?

Answer 1

Here is the missing information.

An exhausted bicyclist pedal somewhat erraticaly when exercising on a static bicycle. The angular velocity of the wheels takes the equation ω(t)=at − bsin(ct) for t≥ 0, where t represents time (measured in seconds), a = 0.500 rad/s2 , b = 0.250 rad/s and c = 2.00 rad/s .

Answer:

0.793 rad

Step-by-step explanation:

From the given question:

The angular velocity of the wheel is expressed by the equation:

`\omega (t) =(d\theta)/(dt)`

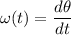
The angular velocity of the wheels takes the description of the equation ω(t)=at−bsin(ct)

SO;

`(d \theta)/(dt) = at - b \ sin \ ct`

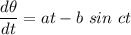
dθ = at dt - (b sin ct) dt

Taking the integral of the above equation; we have:

`\int \limits^(\theta)_(0) \ d \theta = \int \limits ^(t=2)_(0) at \ dt - (b \ sin \ ct) \dt`

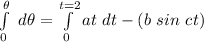
`[\theta] ^(\theta)_(0) = a \bigg [(t^2)/(2) \bigg]^2_0 - \bigg[ -(b)/(c) \ cos \ ct \bigg] ^2_0`

where;

a = 0.500 rad/s2 ,

b = 0.250 rad/s and

c = 2.00 rad/s

`\theta = (0.500 \ rad/s^2 ) \bigg [((2s)^2)/(2) \bigg] - \bigg[ -(0.250 \ rad/s)/(2.00 \ rad/s) \ cos \ (2.00 \ rad/s )( 2.00 \ s) \bigg] - \bigg [ (0.250 \ rad/s)/(2.00 \ rad/s)\bigg ] cos 0^0`

`\mathbf{\theta = 0.793 \ rad}`

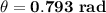
Hence, the angular displacement after two seconds = 0.793 rad