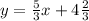Answer:
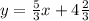
Explanation:
slope-intercept form: y = mx + b
Given:
Slope(m) =
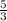
Point = (-1, 3)
To write the equation in slope-intercept form we need to know the slope(m) and the y-intercept(b). Since we already know the value of m, we can use it and the given point to find b:
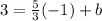
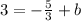
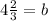
Now that we know the values of b and m, we can write the equation: