Answer:
The function
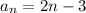 describes the arithmetic sequence.
describes the arithmetic sequence.
Explanation:
Given the sequence
-1, 1, 3, 5, 7, 9, 11, 13
An arithmetic sequence has a constant difference 'd' is defined by
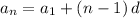
Compute the differences between all the adjacent terms:
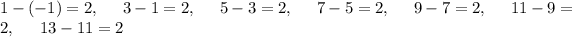
As the difference between all of the adjacent terms is the same and equal to
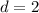
As the first element is
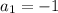
so the term will be:
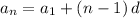
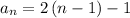
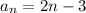
So, the function
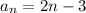 describes the arithmetic sequence.
describes the arithmetic sequence.