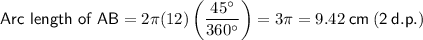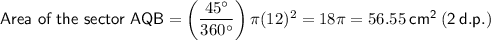Answer:
Arc Measure: equal to the measure of its corresponding central angle.
Formulas
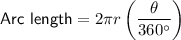
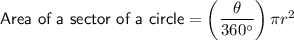

Question 39
Given:
- r = 7 in
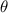 = 90°
= 90°
Substitute the given values into the formulas:
Arc AB = 90°
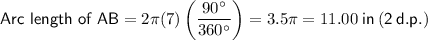
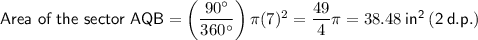
Question 40
Given:
- r = 6 ft
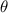 = 120°
= 120°
Substitute the given values into the formulas:
Arc AB = 120°
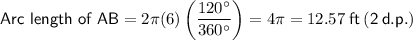
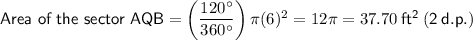
Question 41
Given:
- r = 12 cm
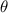 = 45°
= 45°
Substitute the given values into the formulas:
Arc AB = 45°