Question

2.

Two radar stations reconnoiter a plane at the same time. The angles
of elevation to the plane are 20° and 59º. How far apart are the two
radar stations if the plane is at an altitude of 30 km?
km (round to two decimal places)
20
59
30 km
Enter the answer

Answer 1

The distance apart of the two planes is either 100.45 km or 64.40 km

Explanation:

The given parameters are;

The angle of elevation of the plane from the two radar stations are; 20° and 59°

The altitude of the plane = 30 km

The horizontal distance from each of the radar stations from the plane is given as follows;

`tan(\theta) = (Altitude \ of \ the \ plane)/(The \ horizontal \ distance \ of \ radar \ station \ from \ the \ plane)`

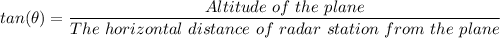
Therefore, we have;

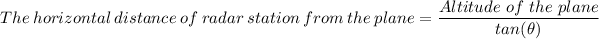`The \ horizontal \ distance \ of \ radar \ station \ from \ the \ plane = (Altitude \ of \ the \ plane)/(tan(\theta))`For each of the given radar stations, and their elevations, we have;

`The \ horizontal \ distance \ of \ the \ 1st \ radar \ station \ from \ the \ plane = (30 \ km)/(tan(20^(\circ)))`

`The \ horizontal \ distance \ of \ the \ 2nd \ radar \ station \ from \ the \ plane = (30 \ km)/(tan(59^(\circ)))`

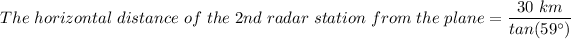
The distance between the two radar stations, d = The sum of their horizontal distances from the plane

Therefore;

`d = (30 \ km)/(tan(20^(\circ))) + (30 \ km)/(tan(59^(\circ))) \approx 100.45 \ km`

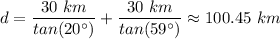
However, when the radar stations are on the same side, we have;

The distance between the two radar stations, dₓ = The difference of their horizontal distances from the plane

`d_x = (30 \ km)/(tan(20^(\circ))) - (30 \ km)/(tan(59^(\circ))) \approx 64.40 \ km`

The distance apart of the two planes is either 100.45 km or 64.40 km