Question

Show that the equation x^3+7x-4=0 has a solution between x=0 and x=1

Answer 1

Explanation:

Using the Intermediate Value Theorem, the following is applied:

"If f(x) is a continuous on interval [a,b] and we have two points f(a) and f(b) then there must be some value c such that f(a)<f(c)<f(b).

So here there must be a c such that

`f(0) < f(c) < f(1)`

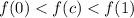
Note: F(c)=0, the questions that the function have a solution between 0 and 1, so that means we must have some value, c such that f(c)=0 that exists

Next, plug in the x values into the function

`f(0) = - 4`

`f(1) = {1}^(3) + 7(1) - 4 = 4`

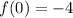
Since cubic functions are continuous and -4<0<4, then there is a solution c that lies between f(0) and f(1)