Question

NO LINKS!!! Find the area of the shaded figure shown. Part 3.#16 & 17. Show work please.

​

Answer 1

16) 240.52 m² (2 dp)

17) 73.06 ft² (2 dp)

Explanation:

Question 16

To calculate the shaded area, subtract the area of the rectangle from the area of the circle. (We know it's a rectangle since the opposite sides are equal in length - marked by dashes).

`\begin{aligned}\textsf{Area of a rectangle}& =\sf width * length\\\implies \sf A& = \sf 20 * 21\\& = \sf 420\:\:m^2\end{aligned}`

To find the area of the circle, first find the radius.

From inspection of the diagram, the diagonal of the rectangle is the diameter of the circle. Therefore, the radius is half the diagonal.

To find the length of the diagonal, use Pythagoras' Theorem:

`\begin{aligned}\sf a^2+b^2 & = \sf c^2\\\implies 20^2+21^2 & = \sf c^2\\\sf c^2 & = 841\\\sf c & =√(841)\\\sf c & = 29\end{aligned}`

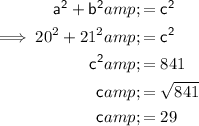
Therefore:

`\begin{aligned}\implies \sf radius & = \sf (1)/(2)c\\\\& = \sf (1)/(2)(29)\\\\& = \sf1 4.5\:m\end{aligned}`

`\begin{aligned}\textsf{Area of a circle} & = \sf \pi r^2\\\implies \sf A & = \sf \pi (14.5)^2\\& = \sf 210.25\pi \:\:m^2\end{aligned}`

Finally:

`\begin{aligned}\textsf{Shaded area} & = \textsf{area of circle}-\textsf{area of rectangle}\\& = \sf 210.25 \pi - 420\\& = \sf 240.52\:\:m^2\:(2\:d.p.)\end{aligned}`

Question 11

To calculate the shaded area, subtract the area of the square from the area of the circle. (We know it's a square as the side lengths are equal - marked by one dash on each side length).

`\begin{aligned}\textsf{Area of a circle} & = \sf \pi r^2\\\implies \sf A & = \sf \pi \left((16)/(2)\right)^2\\& = \sf 64\pi \:\:ft^2\end{aligned}`

To find the area of the square, first find the side length using Pythagoras' Theorem:

`\begin{aligned}\sf a^2+b^2 & = \sf c^2\\\implies 2a^2 & = \sf 16^2\\\sf a^2 & = 128\\\sf a & =√(128)\\\sf a & = 8√(2)\:\:\sf ft\end{aligned}`

`\begin{aligned}\textsf{Area of a square} & = \sf a2\\\implies \sf A & = \sf (8√(2))^2\\& = \sf 128 \:\:ft^2\end{aligned}`

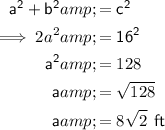
Finally:

`\begin{aligned}\textsf{Shaded area} & = \textsf{area of circle}-\textsf{area of square}\\& = \sf 64 \pi - 128\\& = \sf 73.06\:\:ft^2\:(2\:d.p.)\end{aligned}`