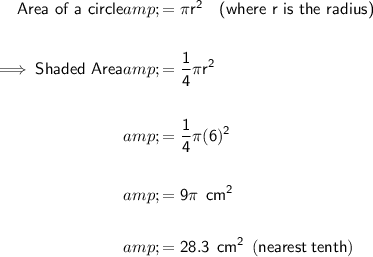Question

NO LINKS!!!

#10 & 11. Find the shaded area figure shown. SHOW WORK PLEASE!!

​

Answer 1

#1

Perpendicular of right angles triangle

• p²=34²-16²
• p²=30²
• p=30

Area of triangle

• 1/2(30)(16)
• 15(16)
• 240units²

Area of rectangle

• 34(21)
• 714units²

Area of shaded region

• 714-240
• 474units²

#11

Area of shaded region

• πr²/4
• π(6)²/4
• 36π/4
• 9π
• 28.3cm²

Answer 2

10) 474 units²

11) 28.3 cm² (nearest tenth)

Explanation:

Question 10

To calculate the shaded area, subtract the area of the triangle from the area of the rectangle.

First, find the base of the triangle using Pythagoras' Theorem:

a² + b² = c²

(where a and b are the legs, and c is the hypotenuse of a right triangle)

Given:

• a = 16
• c = 34

Substituting the given values into the formula to find the base of the triangle:

⇒ a² + b² = c²

⇒ 16² + b² = 34²

⇒ b² = 34²- 16²

⇒ b² = 900

⇒ b = √(900)

⇒ b = 30

Area of triangle = 1/2 × base × height

= 1/2 × 30 × 16

= 240 units²

Area of rectangle = width × length

= 21 × 34

= 714 units²

Shaded area = area of rectangle - area of triangle

= 714 - 240

= 474 units²

Question 11

The central angle of the shaded area is a right angle = 90°

Angles around a point sum to 360°

`\implies \sf (90^(\circ))/(360^(\circ))=(1)/(4)`

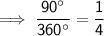
Therefore, the shaded area is a quarter of the area of the circle.

`\begin{aligned}\textsf{Area of a circle} & = \sf \pi r^2 \quad \textsf{(where r is the radius)}\\\\\implies \textsf{Shaded Area} & = \sf (1)/(4)\pi r^2\\\\& = \sf (1)/(4)\pi (6)^2\\\\& = \sf 9\pi \:\:cm^2\\\\& = \sf 28.3\:\:cm^2\:\:(nearest\:tenth)\end{aligned}`