a) The first integral corresponds to the area under y = f(x) on the interval [0, 3], which is a right triangle with base 3 and height 5, hence the integral is
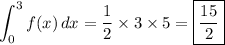
b) The integral is zero since the areas under the curve over [3, 4] and [4, 5] are equal but opposite in sign. In other words, on the interval [3, 5], f(x) is symmetric and odd about x = 4, so
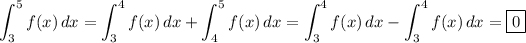
c) The integral over [5, 9] is the negative of the area of a rectangle with length 9 - 5 = 4 and height 5, so
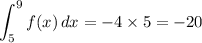
Then by linearity, we have
