Use the rules of exponents and logarithms to solve the equation.
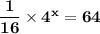
Multiply both sides by 16.
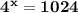
Take the logarithm of the two sides of the equation.
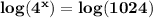
The logarithm of a number raised to a power is the power multiplied by the logarithm of the number.
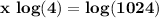
Divide the two sides by log(4).
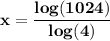
By the base change formula
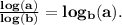
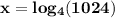
x = 5 ====> Answer