Question

A. find the tangent ratio of angle FKG

b. find the tangent ratio of angle BKG
c. find the tangent ratio of angle KDF
d. find the tangent ratio of angle BCK
e. find the XY coordinates of point g with the center k

use the image to find the answers for each part mathematics high school done​

Answer 1

a. tan∠FKG = √3

b. tan∠BKG = 1

c.
`tan\angle KDF = (1)/(√(3) )`

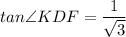
d. tan∠BCK = 1

e. The coordinates of the point g is (4, 4·√3)

Explanation:

a. The trigonometric ratio for tan is given as follows;

`tan\angle X = (Opposite \ leg \ length)/(Adjacent\ leg \ length)`

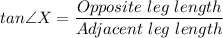
Therefore, we have;

`tan\angle FKG = (Opposite \ leg \ length)/(Adjacent\ leg \ length) = tan(60^(\circ)) = (sin(60^(\circ)))/(cos(60^(\circ)) ) = ((√(3) )/(2) )/((1)/(2) ) = √(3)`

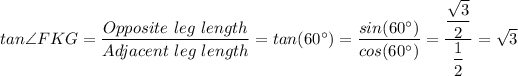
b.

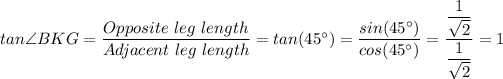
`tan\angle BKG = (Opposite \ leg \ length)/(Adjacent\ leg \ length) = tan(45^(\circ)) = (sin(45^(\circ)))/(cos(45^(\circ)) ) = ((1 )/(√(2) ) )/((1)/(√(2) ) ) = 1`

c.

`tan\angle KDF = (Opposite \ leg \ length)/(Adjacent\ leg \ length) = tan(30^(\circ)) = (sin(30^(\circ)))/(cos(30^(\circ)) ) = ((1 )/(2 ) )/((√(3) )/(2 ) ) = (1)/(√(3) )`

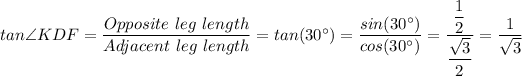
d. In right triangle, ΔBKC, ∠BCK = ∠BKC = 45°

∴ tan(∠BCK) = tan(45°) = 1

e. The x-coordinate of the point g is 4

The y-coordinate of the point g is 4 × tan(60°) = 4·√3

The coordinates of the point g is (4, 4·√3).