Question

Determine if ƒ(x) = –x3 – x4 – 9 + 6x is a polynomial function. If it is, state the degree and the leading coefficient. If not, state why.

Answer 1

The given function is a polynomial function.

The degree of the function is 4 and leading co-efficient is -1.

Explanation:

Given function is:

ƒ(x) = –x^3 – x^4 – 9 + 6x

Putting the terms in order of their power.

`f(x) = -x^4-x^3+6x-9`

A polynomial is an algebraic expression which involves only positive integer exponents for the variables.

A polynomial function is of the form:

`p(x) = a_nx_n+a_(n-1)x^(n-1)+a_(n-2)x^(n-2)........ a_0`

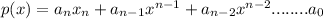
We can see that the function has no negative exponent. So the given function is a polynomial function.

The degree of a polynomial is the highest exponent of variable involved and leading co-efficient is the co-efficient of the variable with highest power.

Hence,

The given function is a polynomial function.

The degree of the function is 4 and leading co-efficient is -1.