Answer:
a) F₃ = 109.5 N , θ₃ = 38.35, b) m = 0.429 kg
Step-by-step explanation:
For this force addition exercise, let's decompose the forces into a coordinate system
strength 1
cos 70 = F₁ₓ / F₁
sin 70 =
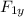 / F₁
/ F₁
F₁ₓ = F₁ cos 70
F_{1y} = F₁ sin 70
F₁ₓ = 45 cos 70 = 15.39 N
F_{1y} = 45 sin70 = 42.29 N
Strength 2
cos 20 = F₂ₓ / F₂
sin 20 = F_{2y} / F₂
F₂ₓ = F₂ cos 20
F_{2y} = F₂ sin20
F₂ₓ = 75 cos 20 = 70.48 N
F_{2y} = 75 sin 20 = 25.65 N
a) in the first part we are asked to find the magnitude of force 3 so that the body is in equilibrium
X axis
∑ Fₓ = 0
F₁ₓ + F₂ₓ + F₃ₓ = 0
F₃ₓ = - F₁ₓ - F₂ₓ
F₃ₓ = - 15.39 - 70.48
F₃ₓ = - 85.87 N
Y Axis
∑ F_{y} = 0
F_{1y} + F_{2y} +F_{3y} = 0
F_{3y} = - F_{1y} -F_{2y}
F_{3y} = - 42.29 - 25.65
F_{3y} = - 67.94 N
the magnitude of this force can be found using the Pythagorean theorem
F₃ = √ (F₃ₓ² + F_{3y}^2)
F₃ = √ (85.87² + 67.94²)
F₃ = 109.5 N
The direction of this force can be found using trigonometry
tan θ = F₃ =
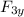 / F₃ₓ
/ F₃ₓ
θ₃ = Tan⁻¹ (67.94 / (85.87))
θ₃ = 38.35º
since the two vectors are negative this angle is in the third quadrant, measured from the positive side of the x axis is
θ₃ = 180 + 38.53
θ₃ = 218.35º
b) I think you have an error in your statement, we have two possibilities:
1) If we eliminate the third force, what is the mass
it should say: "if we apply the third force force ...", they ask that we find the masses of the vehicle, let's use Newton's second law
X axis
F₁ₓ + F₂ₓ = m a
15.39 + 70.48 = m 200
m = 85.87 / 200
m = 0.429 kg
2) If the force F3 is in the first quadrant
F1x + F2x + F3x = m a
m = (15.39 + 70.48 + 85.87) / 200
m = 0.8587 kg