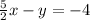Write an equation in standard form for the line, where the points (-2, -1) and (0, 4) are on the line

Question

asked Feb 24, 2021 208k views

1 Answer

Badcompany · Answer 1 · 2021-02-28T21:13:40+0000

Answer:

An equation in standard form for the line is:

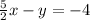
(5)/(2)x-y=-4

Explanation:

Given the points

The slope between two points

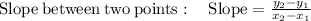
$\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)$

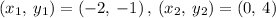
$\left(x_1,\:y_1\right)=\left(-2,\:-1\right),\:\left(x_2,\:y_2\right)=\left(0,\:4\right)$

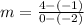
$m=(4-\left(-1\right))/(0-\left(-2\right))$

m=(5)/(2)

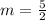
Writing the equation in point-slope form

As the point-slope form of the line equation is defined by

$y-y_1=m\left(x-x_1\right)$

Putting the point (-2, -1) and the slope m=1 in the line equation

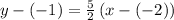
$y-\left(-1\right)=(5)/(2)\left(x-\left(-2\right)\right)$

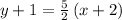
$y+1=(5)/(2)\left(x+2\right)$

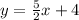
y=(5)/(2)x+4

Writing the equation in the standard form form

As we know that the equation in the standard form is

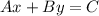
Ax+By=C

where x and y are variables and A, B and C are constants

so

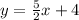
y=(5)/(2)x+4

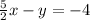
(5)/(2)x-y=-4

Therefore, an equation in standard form for the line is:

(5)/(2)x-y=-4