Question

Identify the y-intercept and the axis of symmetry for the graph of f(x) = 10x^2 + 40x + 42.

a
42; x = 4
b
42; x = –2
c
–42; x = 2
d
0; x = –4

Answer 1

b)42, x=-2

Explanation:

Answer 2

The option 'b' is correct.

Explanation:

Given the function

`f\left(x\right)\:=\:10x^2\:+\:40x\:+\:42`

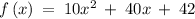
Determining the y-intercept

The y-intercept can be obtained by setting the value x = 0

`y\:=\:10x^2\:+\:40x\:+\:42`

`y\:=\:10\left(0\right)^2\:+\:40\left(0\right)\:+\:42`

`= 0+0+42`

`=42`

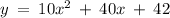
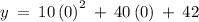
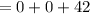
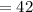
Therefore, the y-intercept is:

• (0, 42)

Determining the axis of symmetry

Given the equation

`y=\:10x^2\:+\:40x\:+\:42`

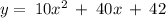
For a parabola in standard form
`y=ax^2\:+\:bx\:+c`

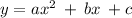
the axis of symmetry is the vertical line that goes through the vertex

`x=(-b)/(2a)`

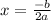
so

The axis of symmetry for
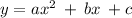`y=ax^2\:+\:bx\:+c` is
`x=(-b)/(2a)`

`a=10,\:b=40`

`x=(-b)/(2a)`

`x=(-40)/(2\cdot \:10)`

`x=-2`

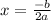
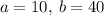
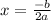
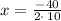
Therefore, the option 'b' is correct.