Question

What is the volume of the geometric solid produced by the triangle below

when it is rotated 360 degrees about the vertical axis YZ? *

Answer 1

The volume of the geometric solid produced is 391 cubic cm ⇒ A

Explanation:

When a right triangle is rotated about its vertical leg 360°, then it formed a cone its radius is the horizontal leg of the triangle and its height is the vertical lege of the triangle.

The rule of the volume of the cone is V =
`(1)/(3)` π r² h, where

• r is the radius of its base

• h is the length of its height

∵ Triangle XYZ is rotated 360° about the vertical side YZ

∴ It formed a cone with a radius = XZ and a height = YZ

∵
`(YZ)/(XZ)=tan(60)`

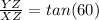
∵ YX = 6√3

∴
`(6√(3))/(XZ)=tan(60)`

∵ tan(60) = √3

∴
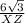`(6√(3))/(XZ)` = √3

→ By using cross multiplication

∴ 6√3 = XZ(√3)

→ Divide both sides by √3

∴ 6 = XZ

∵ XZ = r and YZ = h

∴ r = 6 and h = 6√3

→ By using the rule of the cone above

∵ V =
`(1)/(3)` (π) (6)² (6√3)

∴ V ≅ 391 cm³

∴ The volume of the geometric solid produced is 391 cubic cm