Answer:
The average rate of change of the function
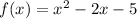 for interval
for interval
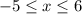 is -1
is -1
Explanation:
We are given function
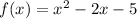 and we need to determine the average rate of change of the function for interval
and we need to determine the average rate of change of the function for interval
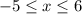
The formula used to find average rate of change is:
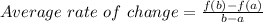
We are given b=6 and a=-5
We need to find f(b) and f(a)
Finding f(b)
Putting x= 6 to find f(b)
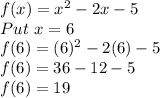
So, f(b)=19
Now finding f(a)
Putting x= -5 to find f(a)
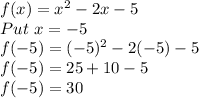
So, f(a)= 30
Finding average rate of change
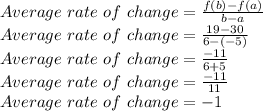
Average rate of change = -1
So, average rate of change of the function
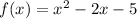 for interval
for interval
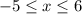 is -1
is -1