Answer:
The slope of line through (2, 4) and (5, 1) is Negative
The slope of line through (3,5) and (-1,2) is Positive
The slope of line through (-7, 8) and (-7,0) is Undefined
The slope of line through (6.-3) and (4, -3) is Zero
Explanation:
Slope is defined as the steepness of a line.
Slope is denoted by m and the formula for calculating slope is:
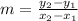
Here
(x1,y1) and (x2,y2) are coordinates of the points through which the line passes
Now,
For (2, 4) and (5, 1):
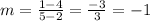
NEGATIVE
For (3,5) and (-1,2)
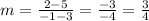
POSITIVE
For (-7, 8) and (-7,0)
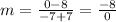
UNDEFINED
For (6.-3) and (4, -3)
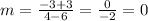
ZERO
Hence,
The slope of line through (2, 4) and (5, 1) is Negative
The slope of line through (3,5) and (-1,2) is Positive
The slope of line through (-7, 8) and (-7,0) is Undefined
The slope of line through (6.-3) and (4, -3) is Zero