Question

-4y=-2x+8 and 3x-6y=6
Perpendicular, parallel, or neither?

Answer 1

The two lines are parallel

Explanation:

• Parallel lines have equal slopes and different y-intercepts

• The product of the slopes of the perpendicular lines is -1 which means if the slope of one is m, then the slope of the other is
  `-(1)/(m)` (reciprocal m and change its sign)

• The slope of the equation ax + by = c is m =
  `(-a)/(b)`

• The slope of the equation by = ax + c is m =
  `(a)/(b)`

Let us use these rules to solve the question

∵ The 1st equation is -4y = -2x + b

∴ a = -2 and b = -4

∵ m =
`(a)/(b)` in this form of the equation

∴ m =
`(-2)/(-4)`

∴ m1 =
`(1)/(2)`

∵ The 2nd equation is 3x - 6y = 6

∴ a = 3 and b = -6

∵ m =
`(-a)/(b)` in this form of the equation

∴ m =
`(-3)/(-6)`

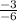
∴ m2 =
`(1)/(2)`

∵ m1 = m2

∴ The slopes of the two lines are equal

→ That means the two lines are parallel

∴ The two lines are parallel