Question

Please at least help me with one of them cause I have no idea

Solve for r:

`v = (4)/(3){r}^(3)`
Solve for v2

`a \: ave = (v2 - v1)/(t2 - t1)`

​

Answer 1

Solving
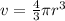`v = (4)/(3)\pi r^3` for r gives us:
`r=\sqrt[3]{(3v)/(4\pi)}`

Solving
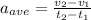`a_(ave) = (v_2-v_1)/(t_2-t_1)` for v2 gives us:
`v_2 = (t_2-t_1)a_(ave)+v_1`

Explanation:

Solving an equation for a variable or constant means that we have to isolate the value on one side of the equation or write the whole equation in terms of that variable or constant.

Now,

Solving
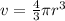`v = (4)/(3)\pi r^3` for r

`v = (4)/(3)\pi r^3`

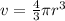
Multiplying whole equation by 3/4

`(3)/(4).v = (3)/(4).(4)/(3) \pi r^3`

`(3)/(4)v = \pi r^3`

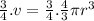
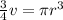
Dividing by Pi on both sides

`(3v)/(4\pi) = (\pi r^3)/(\pi)\\(3v)/(4\pi) = r^3`

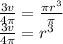
Taking cube root on both sides

`\sqrt[3]{r^3} = \sqrt[3]{(3v)/(4\pi)} \\r = \sqrt[3]{(3v)/(4\pi)}`

Now

Solving
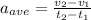`a_(ave) = (v_2-v_1)/(t_2-t_1)` for v2

Multiplying both sides by (t2-t1)

`(t_2-t_1)a_(ave) = (v_2-v_1)/(t_2-t_1)(t_2-t_1)\\(t_2-t_1)a_(ave) = v_2-v_1`

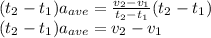
Adding v1 on both sides

`(t_2-t_1)a_(ave)+v_1 = v_2-v_1+v_1\\(t_2-t_1)a_(ave)+v_1 = v_2`

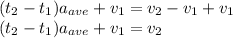
Hence,

Solving
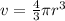`v = (4)/(3)\pi r^3` for r gives us:
`r=\sqrt[3]{(3v)/(4\pi)}`

Solving
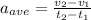`a_(ave) = (v_2-v_1)/(t_2-t_1)` for v2 gives us:
`v_2 = (t_2-t_1)a_(ave)+v_1`