Question

1. Given the following geometric sequence: 10.9, 5.45, 2.725, ...

(a)
Is this a geometric sequence or an arithmetic sequence? Explain.
(b)
Find the 7 th term of the sequence.
(c)
Find the sum of the first 7 terms.

Answer 1

a. This is a geometric sequence because the common ratio is same.

b. 7th term is: 0.1703

c. Sum of 7 terms is: 21.6296875

Explanation:

Given sequence is:

10.9, 5.45, 2.725, ...

Here

a1 = 10.9

a2 = 5.45

a3 = 2.725

We can clearly see that the difference between consecutive terms is not same so it is not an arithmetic sequence

So now common ratio will be found to check if it is a geometric sequence.

Common ratio is the ratio between consecutive terms of a geometric sequence.

So

`r = (5.45)/(10.9) = (2.725)/(5.45) = 0.5`

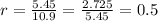
The common ratio is same so the given sequence is a geometric sequence.

The rule for geometric sequence is:

`a_n = a_1 . r^((n-1))`

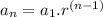
Putting the values, we know

`a_n = 10.9* (0.5)^(n-1)`

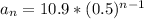
Now for finding 7th term, putting n=7

`a_7 = 10.9 * (0.5)^(7-1)\\a_7 = 10.9 * 0.5^6\\a_7 = 10.9 * 0.015625\\a_7 = 0.1703`

The sum of geometric sequence is given by:

`S_n = (a(r^n-1))/(r-1)\\S_7 = (10.9(0.5^7-1))/(0.5-1)\\S_7 = (10.9(-0.9921875))/(-0.5)\\=(-10.81484375)/(-0.5)\\=21.6296875`

Hence,

a. This is a geometric sequence because the common ratio is same.

b. 7th term is: 0.1703

c. Sum of 7 terms is: 21.6296875