Answer:
a) F₃ = 108.71 N , θ = 218.68º b) m = 0.8487 kg
Step-by-step explanation:
a) To solve this problem we will use Newton's second law, in the first part the accuracy is zero
∑ F = 0
X axis
F₁ₓ + F₂ₓ + F₃ₓ = 0
F₃ₓ = - F₁ₓ -F₂ₓ
Y axis
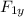 + F_{2y} + F_{3y} = 0
+ F_{2y} + F_{3y} = 0
F3y = -F_{1y} -F_{2y}
Let's use trigonometry to find the components of the applied forces
cos 70 = F₁ₓ / F₁ F₁ₓ = F₁ cos 70
sin 70 = F_{1y} / F₁ F_{1y} = F₁ sin 70
cos 20 = F₂ₓ / F2 F₂ₓ = F₂ cos 70
sin 20 = F_{2y} / F₂ F_{2y} = F₂ sin 70
F₁ₓ = 45 cos 70 = 15.39 N
F_{1y} = 45 sin 70 = 42.29 N
F₂ₓ = 75 cos 20 = 70.48 N
F_{2y} = 75 sin 20 = 25.65 N
let's calculate
F₃ₓ = -15.39 - 70.48
F₃ₓ = -85.87 N
F_{3y} = -42.29 - 25.65
F_{3y} = -67.94 N
this is the force that must be applied to keep the system in equilibrium, we can give this value in the form of module and angle
F₃ = √ (F₃ₓ² + F_{3y}²)
F₃ = √ (85.87² +67.94²)
F₃ = 108.71 N
tan θ = F₃ =
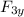 / F₃ₓ
/ F₃ₓ
θ = tan⁻¹ (67.94 / 84.87)
θ = 38.68º
Since the two values are negative, this angle is in the third quadrant, therefore the measuring angle n counterclockwise from the positive side of the x-axis is
θ = 180 + 38.68
θ = 218.68º
b) It is not clear, but we must suppose that the person exerts this force F3 in the direction of movement, bone at an angle θ= 39.68º, in this case Newton's equation for the x axis remains
F₁ₓ + F₂ₓ + F₃ₓ = m a
m = (F₁ₓ + F₂ₓ + F₃ₓ) / a
let's calculate
m = (15.39 + 7048 + 85.87) / 200
m = 0.8487 kg