Question

let f(x)= p+ 8/x-q. the line x=4 is a vertical asymptote to the graph of f. what is the value of q and p, if the y intercept is (0,4)?

Answer 1

The value of q and p is 4 and -24 respectively.

Explanation:

Being
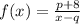`f(x)=(p+8)/(x-q)` , the line x=4 is a vertical asymptote to the graph of f(x). The line r is an asymptote of a function if the graph of the function is infinitely close to the line r. That is, an asymptote is a line to which a function approaches indefinitely, without ever touching it.

Being a rational function that which can be expressed as the quotient of two polynomials, a vertical asymptote occurs when the denominator is 0, that is, where the function is not defined. In this case:

x - q= 0

Solving:

x= q

Being the line x=4 the vertical asymptote, then

4=q

Then the function f (x) is:

`f(x)=y=(p+8)/(x-4)`

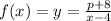
The y intercept is (0,4). This is, x= 0 and y=4. Replacing:

`4=(p+8)/(0-4)`

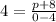
Solving:

`4=(p+8)/(-4)`

4*(-4)= p+8

-16= p+8

-16 - 8= p

-24= p

The value of q and p is 4 and -24 respectively.