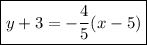Answer:

Explanation:
For it to bisect the segment, we need to find the midpoint.
The midpoint is
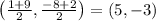
Now, for it to be perpendicular, we need to use the fact that perpendicular lines have slopes that are negative reciprocals of each other.
The slope of the given segment is
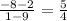 , so the slope of the perpendicular bisector is
, so the slope of the perpendicular bisector is
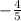
Thus, the equation of the line in point-slope form is