Answer:
The location of the point that is 3/4 the distance from
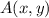 is
is
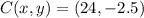 .
.
Explanation:
Let
 and
and
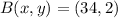 the endpoints of the segment, we can determine the location of the point that is 3/4 the distance from
the endpoints of the segment, we can determine the location of the point that is 3/4 the distance from
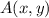 by the following vector equation:
by the following vector equation:
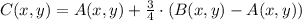 (1)
(1)
If we know that
 and
and
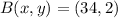 , the location of
, the location of
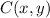 is:
is:
![C(x,y) = (-6,-16)+(3)/(4)\cdot [(34,2)-(-6,-16)]](https://img.qammunity.org/2021/formulas/mathematics/college/6rhhl5z9e56g7wnj4i7uisburcb5olu92o.png)

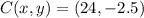
The location of the point that is 3/4 the distance from
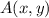 is
is
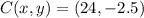 .
.