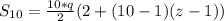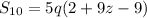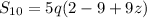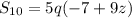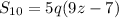Answer:


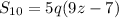
Explanation:
Given
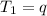
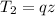
Solving (a1): The common difference (d)
d is calculated as
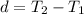
This gives:
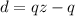
Factorize:

Solving (a2): Sum of n terms
This is calculated using:
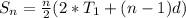
Substitute values for T1 and d
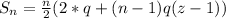
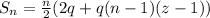
Factorize:
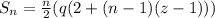

Solving (b): Sum of first 10.
In this case, n = 10
So:

becomes