Question

Consider the function f(x)=10^x and function g(x)=f(x+4). How will the graph of function g differ from the graph of function f?

A. The graph of function g is the graph of function f shifted 4 units to the left.

B. The graph of function g is the graph of function f shifted 4 units to the right.

C. The graph of function g is the graph of function f shifted 4 units up.

D. The graph of function g is the graph of function f shifted 4 units down.

Answer 1

Shifts 4 units to left

Explanation:

Given:

`\displaystyle \large{f(x)=10^x}\\\\\displaystyle \large{g(x)=f(x+4)=10^(x+4)}`

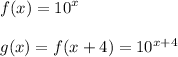
Accorded to transformation rules:

• f(x + a) is shift to left a units.
• f(x - a) is shift to right a units.
• f(x) + a is shift up a units.
• f(x) - a is shift down a units.

Since function g is f(x + 4) then function g is the graph of function f(x) that shifts to left 4 units.