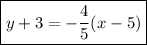Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (1,−8) and (9,2)

Answer 1

Answer:
`y+3=-(4)/(5)(x-5)`

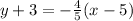
Explanation:

For it to bisect the segment, we need to find the midpoint.

The midpoint is
`\left((1+9)/(2), (-8+2)/(2) \right)=(5, -3)`

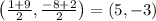
Now, for it to be perpendicular, we need to use the fact that perpendicular lines have slopes that are negative reciprocals of each other.

The slope of the given segment is
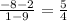`(-8-2)/(1-9)=(5)/(4)`, so the slope of the perpendicular bisector is
`-(4)/(5)`

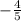
Thus, the equation of the line in point-slope form is
`\boxed{y+3=-(4)/(5)(x-5)}`