Question

6) Two coastguard stations P and Q are 17km apart, with due East of P. A ship S is observed in distress on a bearing 048° fromP and 324 from Q. How far is the ship from each of the coastguard stations?

Answer 1

The ship S is at 10.05 km to coastguard P, and 12.70 km to coastguard Q.

Explanation:

Let the distance of the ship to coastguard P be represented by x, and its distance to coastguard Q be represented by y.

But,

<P = 048°

<Q =
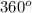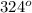
`360^(o)` -
`324^(o)`

= 0
`36^(o)`

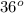
Sum of angles in a triangle =
`180^(o)`

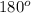
<P + <Q + <S =
`180^(o)`

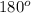
048° + 0
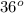`36^(o)` + <S =
`180^(o)`

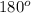
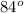`84^(o)` + <S =
`180^(o)`

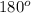
<S =
`180^(o)` -
`84^(o)`

=
`96^(o)`

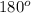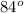
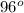
<S =
`96^(o)`

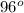
Applying the Sine rule,

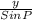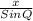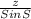
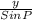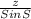
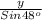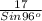
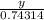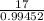
`(y)/(Sin P)` =
`(x)/(Sin Q)` =
`(z)/(Sin S)`

`(y)/(Sin P)` =
`(z)/(Sin S)`

`(y)/(Sin 48^(o) )` =
`(17)/(Sin 96^(o) )`

`(y)/(0.74314)` =
`(17)/(0.99452)`

⇒ y =
`(12.63338)/(0.99452)`

= 12.703

y = 12.70 km

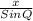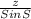
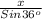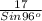
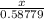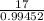
`(x)/(Sin Q)` =
`(z)/(Sin S)`

`(x)/(Sin 36^(o) )` =
`(17)/(Sin 96^(o) )`

`(x)/(0.58779)` =
`(17)/(0.99452)`

⇒ x =
`(9.992430)/(0.99452)`

= 10.0475

x = 10.05 km

Thus,

the ship S is at a distance of 10.05 km to coastguard P, and 12.70 km to coastguard Q.