Question

In ABC the measure of the largest angle 32 less than 3 time the smallest angle the measure of the middle angle is 8 more than half the measure of the largest angle . What is the measure of the middle angle?

Answer 1

Answer: The measure of the middle angle = 52°

Explanation:

Let x = Smallest angle.

largest angle =
`3x-32`

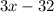
Middle angle=
`8+\frac12 (3x-32)`

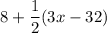
Sum of all angles in a triangle is 180 degrees.

So, Smallest angle+ largest angle+ Middle angle = 180°

`\Rightarrow\ x+8+\frac12 (3x-32)+3x-32=180\\\\\Rightarrow\ 4x-24+(3x)/(2)-16=180\\\\\Rightarrow\ (2*4x+3x)/(2)-40=180\\\\\Rightarrow\ (11x)/(2)-40=180\\\\\Rightarrow\ (11x)/(2)=220\\\\\Rightarrow\ x=(220*2)/(11)\\\\\Rightarrow\ x= 40`

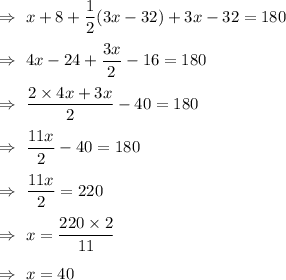
Now , Middle angle=
`8+\frac12 (3(40)-32)=8+\frac12 (120-32)`

`=8+\frac12 (88)\\\\=8+44\\\\=52`

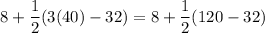
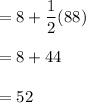
Hence, the measure of the middle angle = 52°