Question

Consider the points A(5, 3t+2, 2), B(1, 3t, 2), and C(1, 4t, 3). Find the angle ∠ABC given that the dot product of the vectors BA and BC is equal to 4. Round your answer to 2 decimal places.

Answer 1

66.42°

Explanation:

Given:

A(5, 3t+2, 2)

B(1, 3t, 2)

C(1, 4t, 3)

BA • BC = 4

Step 1: Find t.

First we have to find vectors BA and BC. We do that by subtracting the coordinates of the initial point from the coordinates of the terminal point.

In vector BA B is the initial point and A is the terminal point.

BA = OA - OB = (5-1, 3t+2-3t, 2-2) = (4, 2, 0)

BC = OC - OB = (1-1, 4t-3t, 3-2) = (0, t, 1)

Now we can find t because we know that BA • BC = 4

BA • BC = 4

To find dot product we calculate the sum of the produts of the corresponding components.

BA • BC = (4)(0) + (2)(t) + (0)(1)

4 = (4)(0) + (2)(t) + (0)(1)

4 = 0 + 2t + 0

4 = 2t

2 = t

t = 2

Now we know that:

BA = (4, 2, 0)

BC = (0, 2, 1)

Step 2: Find the angle ∠ABC.

Dot product: a • b = |a| |b| cos(angle)

BA • BC = 4

|BA| |BC| cos(angle) = 4

To get magnitudes we square each compoment of the vector and sum them together. Then square root.

`|BA| = √(4^2 + 2^2 + 0^2) = √(20) = 2√(5)`

`|BC| = √(0^2 + 2^2 + 1^2) = √(5)`

`2√(5)√(5)\cos{(m\angle{ABC})} = 4`

`10\cos{(m\angle{ABC})} = 4`

`\cos(m\angle{ABC}) = (4)/(10)=(2)/(5)`

`m\angle{ABC} = cos^(-1){((2)/(5))}`

`m\angle{ABC} = 66.4218^(\circ)`

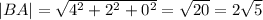
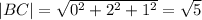
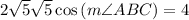
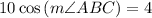
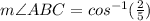
Rounded to two decimal places:

`m\angle{ABC} = 66.42^\circ`