Answer:
209
Explanation:
You would first create an explicit formula for the provided sequence.
The basic explicit formula for arithmetic sequences is
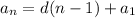 , where an is the number of the term, d is the number you are adding or subtracting by, n the location of the term, and a1 is the first number.
, where an is the number of the term, d is the number you are adding or subtracting by, n the location of the term, and a1 is the first number.
We would then substitute the values given into the formula.
We are trying to solve the value of the 52nd term. This makes n = 52. The first number of the sequence is 5, so a1 is 5. Finally, d is 4 because we are adding 4 to each number in the sequence.
Therefore, our resulting equation would be
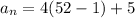 , which equals 209.
, which equals 209.