Question

Consider the feasible region in the xy-plane defined by the following linear inequalities.

x≥0
y ≥0
x ≤ 10
x +y≥ 5
x + 2y ≤ 18
Part 2 Exercises:
1. Find the coordinates of the vertices of the feasible region. Clearly show how each vertex is determined and which lines form the vertex.
2. What is the maximum and the minimum value of the function Q = 60x+78y on the feasible region?

Answer 1

1. (0,5), (0,9), (10,4), (10,0), (5,0)

2.
`Q_(max)=912`

`Q_(min)=300`

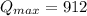
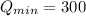
Explanation:

1.

In order to determine the coordinates of the vertices of the feasible region, we must first graph each of the inequalities. The feasible region is the region where all the inequalities cross each other. In this case it's the region shaded on the attached picture.

The first point is the intercept between the equations x=0 and x+y=5 so in order to find this first coordinate we need to substitute x=0 and solve for y.

0+y=5

y=5

(0,5)

The next point is the intercept between the equations x=0 and x+2y=18, so again, we substitute x for zero and solve for y:

0+2y=18

`y=(18)/(2)`

y=9

(0,9)

The next coordinate is the intercept between the lines x=10 and x+2y=18, so we substitute x for 10 and solve for y:

10+2y=18

2y=18-10

2y=8

`y=(8)/(2)`

y=4, so the oint is

(10,4)

The next point is the intercept between the lines x=10 and y=0, so the point is:

(10,0)

The final point is the intercept between the equations: y=0 and x+y=5. We substitute y for zero and solve for x:

x+0=5

x=5

so the point is:

(5,0).

2. In order to determine the maximum and minimum value of the function Q=60x+78y on the feasible region, we must evaluate it for each of the points found on part 1.

(0,5)

Q=60(0)+78(5)

Q=390

(0,9)

Q=60(0)+78(9)

Q=702

(10,4)

Q=60(10)+78(4)

Q=912

(10,0)

Q=60(10)+78(0)

Q=600

(5,0)

Q=60(5)+78(0)

Q=300

So now we compare the answers and pick the minimum and maximum results.

We get that:

`Q_(max)=912`

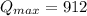
when x=10 and y=4

and

`Q_(min)=300`

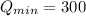
When x=5 and y=0