Question

A study done by researchers at a university concluded that ​% of all student athletes in this country have been subjected to some form of hazing. The study is based on responses from athletes. What are the margin of error and​ 95% confidence interval for the​ study?

Answer 1

The missing digits is highlighted in bold form

A study done by researchers at a university concluded that ​70% of all student-athletes in this country have been subjected to some form of hazing. The study is based on responses from 1800 athletes. What are the margin of error and​ 95% confidence interval for the​ study?

Answer:

Explanation:

Given that:

The sample proportion
`\hat p = 0.70`

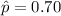
The sample size n = 1800

At 95% confidence interval level:

The level of significance = 1 - 0.95 = 0.05

Critical value:
`Z_(0.05/2) = Z_(0.025) = 1.96`

Thus, the Margin of Error E =
`Z_(\alpha/2) * \sqrt{(\hat p ( 1- \hat p))/(n)}`

`= 1.96 * \sqrt{( 0.70 ( 1-0.70))/(1800)}`

`= 1.96 * \sqrt{( 0.70 ( 0.30))/(1800)}`

`= 1.96 * \sqrt{(0.21)/(1800)}`

`= 1.96 * \sqrt{1.16666667* 10^(-4)}`

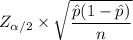
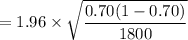
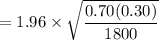
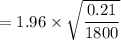
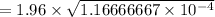
the Margin of Error E = 0.021

At 95% C.I for the population proportion will be:

`= \hat p \pm Z_(\alpha/2) \sqrt{(\hat p(1- \hat p))/(n)}`

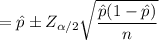
= 0.70 ± 0.021

= (0.70 - 0.021, 0.70 + 0.021)

= 0.679, 0.721)