Question

What is the argument of -5\sqrt{3}+ 5i?

Answer 1

D 150 degrees

Explanation:

got it right on edge

Answer 2

150 degrees

Explanation:

Graphing the complex number we see the angle terminates in the second quadrant. This means the argument, the angle, will be between 90 degrees and 180 degrees.

So if we create a right triangle with that point after graphing it. We see the height of that triangle is 5 because that is the imaginary part. The base of that triangle has length
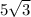`5√(3)`. The problem is this doesn't give us any part of the angle we want, but it does give us the complementary of the part of the angle that is in second quadrant.

Let's find the complementary angle.

So the opposite side of the complementary angle is 5.

The adjacent side of the complementary angle is
`5√(3)`.

`\tan(\theta)=(5)/(5√(3))`

`\tan(\theta)=(1)/(√(3))`

`\theta=\tan^(-1)((1)/(√(3)))`

`\theta=30`

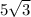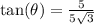
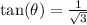
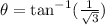
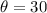
So 90-30=60.

The answer therefore 60+90=150.