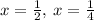Question

solve the following quadratic equation using the quadratic formula and then choose the correct solution set 8x2-6x+1=0

Answer 1

1/4 1/2

Explanation:

Answer 2

The solutions to the quadratic equation using the quadratic formula will be:

`x=(1)/(2),\:x=(1)/(4)`

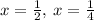
Explanation:

Given the equation

`8x^2-6x+1=0`

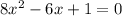
solving with the quadratic formula

`\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}`

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:}\quad a=8,\:b=-6,\:c=1`

`x_(1,\:2)=(-\left(-6\right)\pm √(\left(-6\right)^2-4\cdot \:8\cdot \:1))/(2\cdot \:8)`

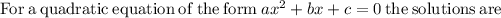
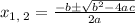
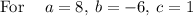
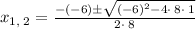
as

`√(\left(-6\right)^2-4\cdot \:8\cdot \:1)=2`

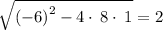
so

`x_(1,\:2)=(-\left(-6\right)\pm \:2)/(2\cdot \:8)`

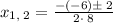
Separating the solution

`x_1=(-\left(-6\right)+2)/(2\cdot \:8),\:x_2=(-\left(-6\right)-2)/(2\cdot \:8)`

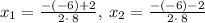
solving

`x_1=(-\left(-6\right)+2)/(2\cdot \:\:8)`

`=(6+2)/(2\cdot \:8)`

`=(8)/(16)`

`=(1)/(2)`

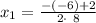
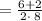
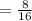
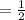
and

`x_2=(-\left(-6\right)-2)/(2\cdot \:8)`

`=(6-2)/(2\cdot \:\:\:8)`

`=(4)/(16)`

`=(1)/(4)`

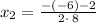
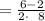
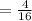
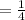
Therefore, the solutions to the quadratic equation using the quadratic formula will be:

`x=(1)/(2),\:x=(1)/(4)`